LearningByDoing Series: Building Blocks of Neural Network - Activation Functions

Activation Functions:

Purpose:
- Activation functions determine the output of a neural network node given an input or set of inputs, introducing non-linear properties to the network enabling them to learn complex patterns.
- Activation functions help decide whether a neuron should be activated or not, influencing the network’s overall decision-making process.
Common functions
1. Sigmoid
2. Tanh
3. ReLU
4. Leaky ReLU
5. Softmax
6. ELU
7. Mish
8. GELU
9. SELU
10. Swish
Choice of Activation Function:
- Depends on the specific application, the nature of the data, and the type of problem being solved.
- For example, ReLU is often used for hidden layers due to its computational efficiency, while softmax is preferred for the output layer in classification tasks.
Challenges:
- Each activation function has its own set of challenges, such as vanishing gradient problem with sigmoid and tanh, or the dying ReLU problem, where neurons stop learning entirely.

Papers for Activation Functions

ReLU (Rectified Linear Unit)
- Vinod Nair and Geoffrey E. Hinton, “Rectified Linear Units Improve Restricted Boltzmann Machines,” in Proceedings of the 27th International Conference on International Conference on Machine Learning (ICML’10), 2010.
Leaky ReLU
- Andrew L. Maas, Awni Y. Hannun, and Andrew Y. Ng, “Rectifier Nonlinearities Improve Neural Network Acoustic Models,” in Proc. ICML, 2013.
ELU (Exponential Linear Unit)
- Djork-Arné Clevert, Thomas Unterthiner, and Sepp Hochreiter, “Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs),” ICLR 2016.
Mish
- Diganta Misra, “Mish: A Self Regularized Non-Monotonic Neural Activation Function,” 2019.
GELU (Gaussian Error Linear Unit)
- Dan Hendrycks and Kevin Gimpel, “Gaussian Error Linear Units (GELUs),” 2016.
SELU (Scaled Exponential Linear Unit)
- Günter Klambauer, Thomas Unterthiner, Andreas Mayr, and Sepp Hochreiter, “Self-Normalizing Neural Networks,” in Advances in Neural Information Processing Systems (NIPS) 2017.
Swish
- Prajit Ramachandran, Barret Zoph, and Quoc V. Le, “Searching for Activation Functions,” 2017.

import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# Use GPU, if available
device = 'cuda' if torch.cuda.is_available() else 'cpu'
print(device)

# Method to plot output of activation functions
def plot_output(data, output, title:str):
    """
    Plots the output of a activation function.
    """

    plt.plot(data.numpy(), output.numpy(), color='green', label=title)
    plt.xlabel("Input")
    plt.ylabel("Output")
    plt.legend(loc='upper left')
    plt.title(title)
    plt.grid(True)
    plt.show()

# sample data
data = torch.linspace(-5, 5, 100)

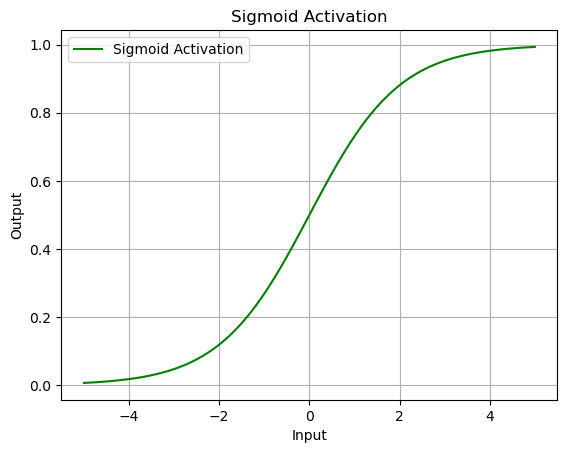
Sigmoid

What is the Sigmoid Function?

Also known as the logistic function
Characterized by its S-shaped curve and is one of the earliest activation functions used in neural networks.
The function maps any real-valued number into a range between 0 and 1, making it especially useful for models where the output is a probability.

When is the Sigmoid Function Used?

Primarily used in binary classification problems within neural networks, especially in the output layer.

What is the Math Formula of the Sigmoid Function?

The mathematical formula of the Sigmoid function is:

\[\sigma(x) = \frac{1}{1 + e^{-x}}\]

where:

$\sigma(x)$ is the output of the sigmoid function,
$ e $ is the base of the natural logarithm (approximately 2.71828),
$ x $ is the input to the function.

Advantages and Disadvantages of the Sigmoid Function

Advantages:

Output Range: The output is bounded between 0 and 1, making it useful for interpreting the output as probabilities.
Smooth Gradient: It provides a smooth gradient, essential for optimization using gradient descent.

Disadvantages:

Vanishing Gradient Problem: For very high or very low values of input, the Sigmoid function saturates, leading to gradients very close to 0. This makes the network hard to train, as it causes the gradient descent to update the weights very slowly.
Not Zero-Centered: The output of the Sigmoid function is not zero-centered. This can lead to the gradient updates going too far in different directions, slowing down the learning process.
Computational Expense: The exponential function present in the sigmoid function is computationally expensive compared to other activation functions like ReLU.

# Sigmoid activation function

sigmoid = nn.Sigmoid()

output = sigmoid(data)

plot_output(data, output, 'Sigmoid Activation')

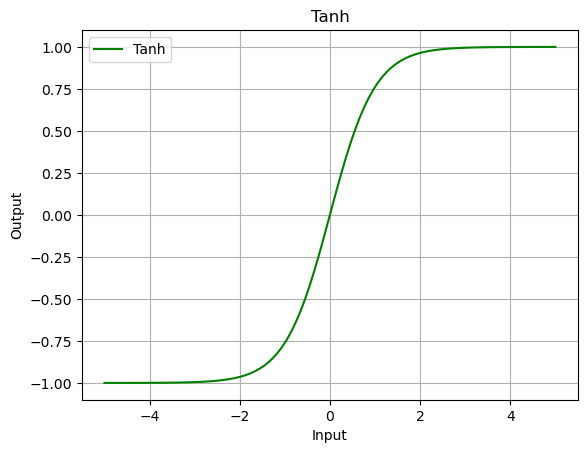
Tanh

What is the Tanh Function?

Short for hyperbolic tangent function, is a type of activation function used in neural networks.
It is similar to the sigmoid function but maps the input values to a range between -1 and 1.
The Tanh function is symmetrical around the origin, which gives it some advantages in certain neural network architectures.

When is the Tanh Function Used?

Used in hidden layers of a neural network because its outputs are zero-centered, making it easier for the model to converge during training.

What is the Math Formula of the Tanh Function?

The mathematical formula of the Tanh function is:

\[\tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}\]

where:

$\tanh(x)$ is the output of the Tanh function,
$e$ is the base of the natural logarithm (approximately 2.71828),
$x$ is the input to the function.

Advantages and Disadvantages of the Tanh Function

Advantages:

Zero-Centered: Unlike the sigmoid function, the output of the Tanh function is zero-centered, which generally helps in making the learning phase more efficient for the network.
Steep Gradient: The Tanh function has a steeper gradient than the sigmoid, which can lead to faster convergence in some cases.

Disadvantages:

Vanishing Gradient Problem: Similar to the sigmoid function, the Tanh function also suffers from the vanishing gradient problem for inputs with large absolute values, which can slow down the training or make it difficult for the network to learn.
Computational Expense: The computation of the exponential function in the Tanh function can be relatively expensive, especially for deep neural networks with a large number of layers.

tanh = nn.Tanh()

output =  tanh(data)

plot_output(data, output, 'Tanh')

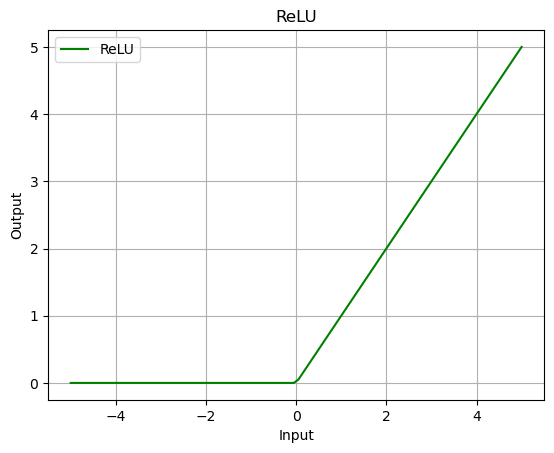
ReLU

What is the ReLU Function?

Standing for Rectified Linear Unit
Widely used activation function in neural networks, especially in deep learning models.
It is a piecewise linear function that outputs the input directly if it is positive; otherwise, it outputs zero.
It has become a default activation function for many types of neural networks because it introduces non-linearity with less likelihood of causing the vanishing gradient problem.

When is the ReLU Function Used?

Commonly used in the hidden layers of neural networks.
Its simplicity and efficiency make it suitable for networks with a large number of layers

What is the Math Formula of the ReLU Function?

The mathematical formula of the ReLU function is:

\[{ReLU}(x) = \max(0, x)\]

where:

$x$ is the input to the function.
The output is $x$ if $x$ is greater than 0; otherwise, it is 0.

Advantages and Disadvantages of the ReLU Function

Advantages:

Computational Simplicity: The ReLU function is computationally efficient, allowing networks to converge faster during training.
Sparsity: ReLU can lead to sparse representations, which are beneficial for neural networks, making them more efficient and easier to train.
Reduces Likelihood of Vanishing Gradient: By providing a linear response for positive inputs, it reduces the chances of the vanishing gradient problem compared to sigmoid or tanh.

Disadvantages:

Dying ReLU Problem: If a large number of activations become negative, then the neuron might stop activating altogether, essentially causing part of the network to die.
Not Zero-Centered Output: The output of ReLU is not zero-centered, which can sometimes be a drawback in optimization.

relu = nn.ReLU()

output = relu(data)

plot_output(data, output, 'ReLU')

LeakyReLU

What is the LeakyReLU Function?

Stands for Leaky Rectified Linear Unit.
It is a variant of the ReLU function designed to allow a small, non-zero gradient when the unit is not active and the input is less than zero.
This modification aims to fix the “dying ReLU” problem, where neurons can sometimes become inactive and stop contributing to the learning process.

When is the LeakyReLU Function Used?

Used in the hidden layers of neural networks as an attempt to overcome the limitations of the traditional ReLU activation function.
It is particularly useful in deep learning models where the dying ReLU problem can impair the training process.

What is the Math Formula of the LeakyReLU Function?

The mathematical formula of the LeakyReLU function is:

\[LeakyReLU(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha x & \text{if } x \leq 0 \end{cases}\]

where:

$x$ is the input to the function,
$\alpha$ is a small constant (e.g., 0.01) that determines the slope of the function for $x\leq 0$.

Advantages and Disadvantages of the LeakyReLU Function

Advantages:

Mitigates the Dying ReLU Problem: By allowing a small gradient when $ x $ is less than zero, LeakyReLU ensures that all neurons have the opportunity to update and learn, reducing the risk of dead neurons during training.
Improved Learning for Deep Networks: The slight gradient for negative input values can help maintain the flow of gradients through the network, improving the training of deep models.

Disadvantages:

Parameter Tuning: The effectiveness of LeakyReLU can depend on the choice of $\alpha$, which may require tuning for optimal performance.
Increased Computational Complexity: While still relatively simple, LeakyReLU is slightly more complex than ReLU due to the additional operation for negative inputs.

L_relu = nn.LeakyReLU(negative_slope=0.1)

output = L_relu(data)

plot_output(data, output, 'Leaky ReLU')

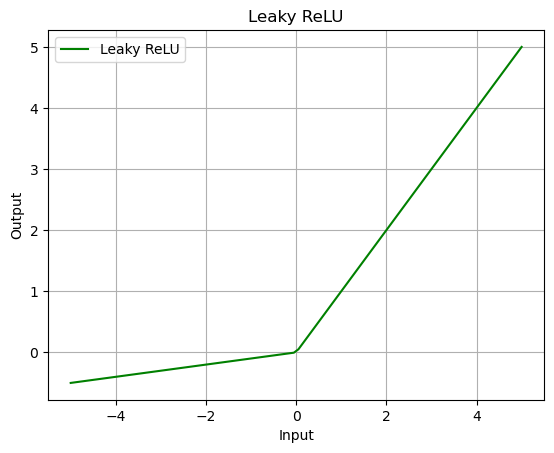
Softmax

What is the softmax function?

The softmax function, also known as the normalized exponential function.
Mathematical function that converts a vector of numbers into a vector of probabilities, where the probabilities of each value are proportional to the relative scale of each value in the vector.

When is the softmax function used?

Primarily used in multiclass classification problems.
Typically placed in the last layer to interpret the outputs as probabilities.
Each value in the output of the softmax function corresponds to the probability that the input example belongs to one of the classes.

What is the mathematical formula of the softmax function?

Given a vector $Z$ of raw class scores from the final layer of a neural network, the softmax function $\sigma(Z)_j$ for a class $j$ is calculated as:

\[\sigma(Z)_j = \frac{e^{Z_j}}{\sum_{k=1}^{K}e^{Z_k}}\]

where:

$e$ is the base of the natural logarithm,
$Z_j$ is the score for class $j$,
$K$ is the total number of classes,
the denominator is the sum of the exponential of all class scores in the vector $Z$.

This formula ensures that all the output values of the softmax function are in the range (0, 1) and sum up to 1, making it a probability distribution.

What are the advantages and disadvantages of softmax?

Advantages:

Interpretability: The softmax function outputs a probability distribution over classes, making the model’s predictions easy to interpret.
Versatility: It can be used in multiple types of classification problems, including binary and multiclass classification.
Differentiable: The softmax function is smooth and differentiable, allowing it to be used in backpropagation when training neural networks.

Disadvantages:

Vulnerability to Overflows: The use of the exponential function can lead to numerical instability, resulting in overflow or underflow errors. This can be mitigated by using techniques such as subtracting the max value from the scores before applying the exponential function.
Does Not Handle Non-Exclusive Classes Well: For multi-label classification problems where an instance can belong to multiple classes simultaneously, softmax may not be appropriate because it assumes each instance is assigned to just one class.
Sensitivity to Outliers: The exponential nature of the softmax function can cause it to be highly sensitive to outliers or very large inputs, leading to skewed distributions.

softmax = nn.Softmax(dim=0)

output = softmax(data)

plot_output(data, output, 'Softmax')

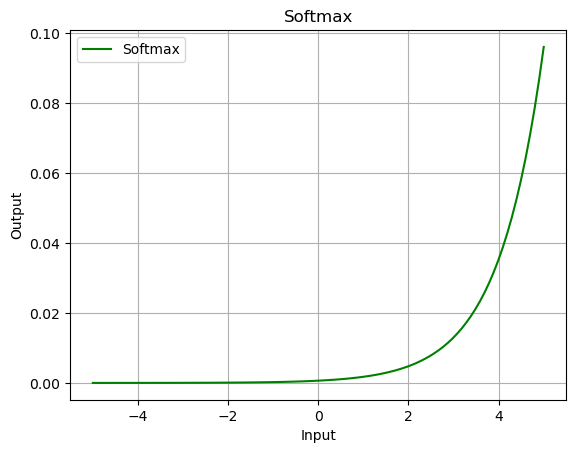
SoftPlus Activation Function

The SoftPlus function, also known as Smooth ReLU
It offers a smoother and more gradual transition compared to the ReLU (Rectified Linear Unit) function, while sharing some of its benefits.

Formula

The mathematical formula for SoftPlus is: $SoftPlus(x) = \ln(1 + \exp(x))$

This function takes any real number $x$ as input and returns the natural logarithm of 1 plus the exponential of $x$.

Usage

SoftPlus is primarily used in hidden layers of neural networks for several reasons:

Smooth gradient: Unlike ReLU, which has a sharp gradient at zero, SoftPlus has a smooth, non-zero gradient throughout its domain. This helps in avoiding the vanishing gradient problem that can hinder learning in deep networks.
Positive outputs: SoftPlus always outputs positive values, which can be beneficial in specific applications like modeling probabilities or dealing with data inherently positive.

Advantages

Smooth gradient: Compared to ReLU, SoftPlus avoids the vanishing gradient problem due to its smooth gradient.
No “dying neurons”: Unlike ReLU, SoftPlus prevents neurons from becoming inactive by always having a positive output.
Numerically stable: SoftPlus is less susceptible to numerical instability compared to other activation functions like sigmoid.

Disadvantages

Computationally less efficient: Compared to ReLU, which is simply a thresholding operation, SoftPlus involves calculating the natural logarithm and exponential, making it slightly computationally expensive.
Not zero-centered: Unlike ReLU and tanh, SoftPlus outputs are always positive, which can lead to imbalanced activations in the network.

softplus = nn.Softplus()

output =  softplus(data)

plot_output(data, output, 'SoftPlus')

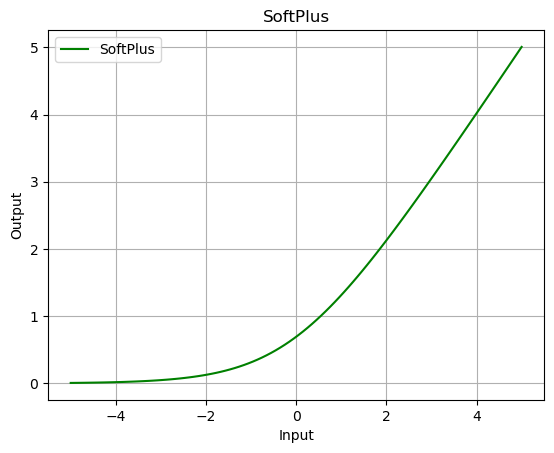
ELU

What is the ELU function?

Exponential Linear Unit (ELU)
Aims to improve the training speed and performance of deep learning models.
It is designed to bring together the best of both ReLU and its variants and the exponential functions.

When is the ELU function used?

ELU is often used in hidden layers of neural networks, particularly in scenarios where the goal is to reduce the vanishing gradient problem that can affect ReLU activations, without introducing the potential for noise in the training process as seen with LeakyReLU or PReLU.
It’s beneficial in deep networks that are prone to slow training or convergence issues due to non-linearities.

What is the mathematical formula of the ELU function?

The ELU function is defined as follows:

\[ELU(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha(e^x - 1) & \text{if } x \leq 0 \end{cases}\]

where:

$x$ is the input to the function,
$\alpha$ is a hyperparameter that defines the value that ELU approaches when $x$ is a large negative number.

What are the advantages and disadvantages of ELU?

Advantages:

Reduction of Vanishing Gradient Problem: Like ReLU and its variants, ELU helps in mitigating the vanishing gradient issue, but with a smoother transition for negative input values.
Better Performance for Deep Networks: ELU can help deep neural networks learn faster and perform better by introducing non-linearity without significantly hindering the learning of patterns in data.
Continuity for All Input Values: ELU is continuous and differentiable at all points, including $x=0$, which aids in more stable and efficient gradient descent optimization.

Disadvantages:

Computational Complexity: The use of the exponential function makes ELU computationally more intensive than ReLU or LeakyReLU, potentially slowing down the training process.
Parameter Tuning: The $\alpha$ parameter needs to be chosen carefully. While a default value of 1 is commonly used, different settings might be required based on the specific application or dataset, adding to the complexity of model design.
Not Zero-Centered for Positive Inputs: Similar to ReLU, the output of ELU for positive inputs is not zero-centered, which can potentially affect the convergence rate of gradient descent algorithms.

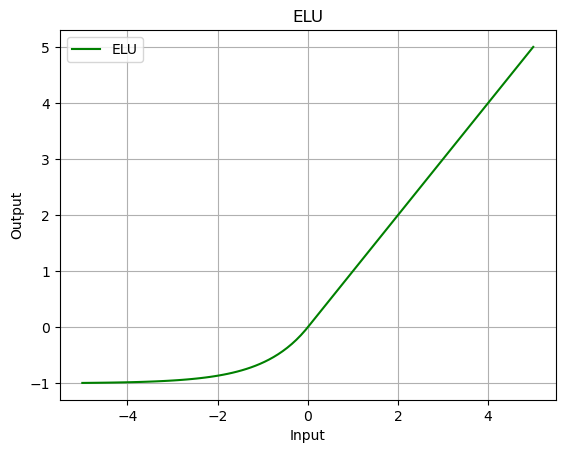
elu = nn.ELU(alpha=1)

output =  elu(data)

plot_output(data, output, 'ELU')

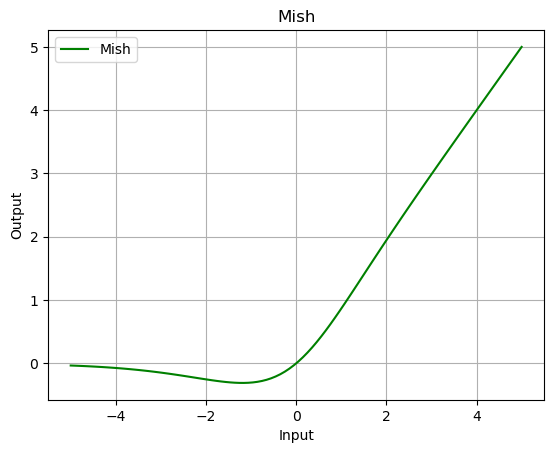
Mish

What is the Mish function?

Mish function is a smooth, non-monotonic activation function
Combines the advantages of ReLU and its variants with a non-linear function to improve model performance and generalization.
It was proposed as a way to enhance the representation capacity of neural networks while maintaining a strong regularization effect.

When is the Mish function used?

Mish is often used in the hidden layers of deep neural networks, particularly in scenarios where the goal is to improve model accuracy and generalization across a wide range of tasks.
Its use is more common in state-of-the-art architectures where the focus is on pushing the boundaries of model performance.

What is the mathematical formula of the Mish function?

The Mish function is defined by the formula:

\[\text{Mish}(x) = x \tanh(\ln(1 + e^x))\]

where:

$x$ is the input to the function,
$\tanh$ is the hyperbolic tangent function,
$\ln(1 + e^x)$ represents the softplus function.

What are the advantages and disadvantages of Mish?

Advantages:

Improved Generalization: Mish has been shown to help neural networks generalize better to unseen data compared to other activation functions.
Self-Regularizing Effect: Mish tends to have a self-regularizing effect that can reduce the need for other forms of regularization, such as dropout.
Smoothness and Non-monotonicity: The smooth, non-monotonic nature of Mish allows for better gradient flow, potentially leading to improved training dynamics and convergence.

Disadvantages:

Computational Complexity: The complexity of the Mish function, due to the combination of exponential, logarithmic, and hyperbolic tangent operations, makes it more computationally intensive than simpler functions like ReLU.
Potential for Slow Training: Due to its computational cost, using Mish in very deep or complex networks can lead to slower training times compared to networks using simpler activation functions.
Hyperparameter Sensitivity: While Mish generally improves model performance, it can make the model more sensitive to the choice of other hyperparameters, such as learning rate and batch size, requiring careful tuning for optimal results.

mish = nn.Mish()

output = mish(data)

plot_output(data, output, 'Mish')

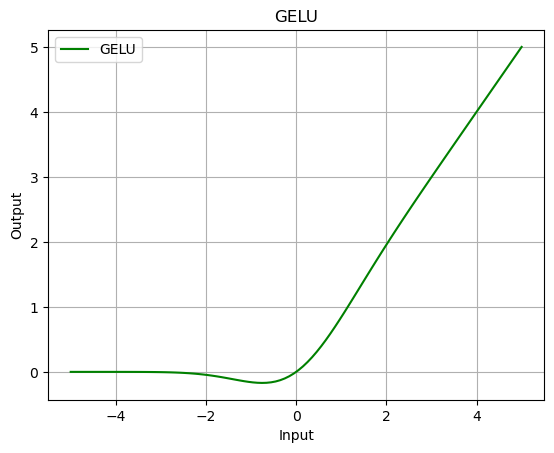
GELU

What is the GELU function?

Gaussian Error Linear Unit (GELU)
Combines properties of both linear and non-linear functions.
It was designed to model the stochastic regularity of neurons in the brain, providing a smoother transition between the activated and non-activated states of a neuron.

When is the GELU function used?

GELU is often used in the hidden layers of deep neural networks, particularly in state-of-the-art models in natural language processing (NLP) and computer vision.
It has gained popularity due to its performance improvements in models like Transformers and BERT.

What is the mathematical formula of the GELU function?

The GELU function can be approximated by the following formula:

\[\text{GELU}(x) = x \Phi(x)\]

where:

$x$ is the input to the function,
$\Phi(x)$ is the cumulative distribution function of the standard normal distribution.

An exact formulation involves more complex operations involving the standard normal cumulative distribution function, but the approximation provided is commonly used due to its simplicity and efficiency.

What are the advantages and disadvantages of GELU?

Advantages:

Improved Learning Dynamics: GELU has been shown to improve the learning dynamics of neural networks by allowing a more flexible shape of the activation function, which can adapt more effectively to different types of data distributions.
Enhanced Model Performance: Models utilizing GELU often achieve higher performance on a variety of tasks, especially in NLP and computer vision, due to its ability to better capture complex patterns in data.
Smooth Gradient Flow: The smooth nature of GELU helps in maintaining a stable and efficient gradient flow during backpropagation, reducing the likelihood of vanishing or exploding gradients.

Disadvantages:

Computational Cost: The calculation of the GELU function is more computationally intensive than simpler functions like ReLU, potentially increasing the training time of models.
Limited Intuition: The complex nature of GELU, being based on the distribution function of the Gaussian, might offer less intuitive understanding compared to more straightforward activations like ReLU or LeakyReLU.
Optimization Sensitivity: Due to its non-linear and non-monotonic properties, GELU might introduce additional sensitivity to the optimization process, requiring careful tuning of hyperparameters for optimal model performance.

gelu = nn.GELU()

output = gelu(data)

plot_output(data, output, 'GELU')

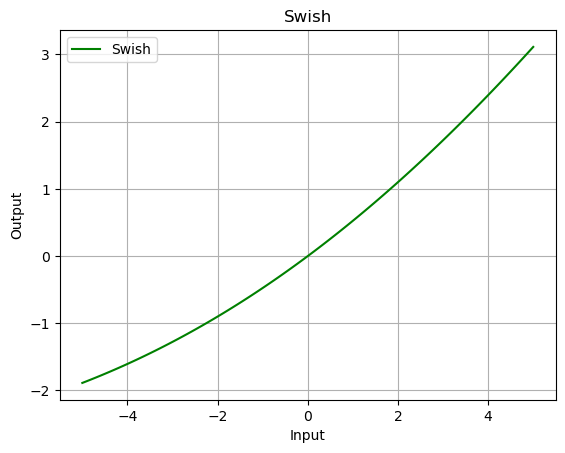
Swish

What is the Swish function?

The Swish function is a defined as the product of the input and the sigmoid of the input.
It was developed based on empirical evidence, showing improved performance on deep learning models over traditional activation functions like ReLU.

When is the Swish function used?

Swish is often used in various layers of deep neural networks, particularly where there is a need for overcoming limitations of ReLU, such as the dying ReLU problem.
It has been applied successfully across a range of tasks, including image recognition and natural language processing.

What is the mathematical formula of the Swish function?

The mathematical formula for the Swish function is:

\[\text{Swish}(x) = x \cdot \sigma(x)\]

where:

$x$ is the input to the function,
$\sigma(x)$ is the sigmoid function, $\sigma(x) = \frac{1}{1 + e^{-x}}$.

What are the advantages and disadvantages of Swish?

Advantages:

Improved Performance: Swish has been shown to outperform ReLU and other activations on a variety of deep learning tasks, leading to better model accuracy and generalization.
Smooth Gradient Flow: Due to its smoothness, Swish allows for a more efficient flow of gradients through the network, potentially reducing issues related to the vanishing gradient problem.
Self-Gating Property: The Swish function has a self-gating property, which means it can control the flow of information in the network without additional gating mechanisms, making the network architecture simpler.

Disadvantages:

Computational Overhead: Swish involves more computation than ReLU due to the presence of the sigmoid function, which can lead to increased training times.
Empirical Basis: The development of Swish is more empirical than theoretical, meaning its effectiveness can vary across different datasets and model architectures without a clear theoretical understanding of why.
Optimization Sensitivity: Like other sophisticated activation functions, Swish might introduce additional sensitivity to the optimization process, requiring careful hyperparameter tuning to achieve optimal performance.

class Swish(nn.Module):
    def __init__(self,beta):
        super(Swish, self).__init__()
        self.beta = beta
        

    def forward(self, input):
        return input * torch.sigmoid(input * self.beta)
    

swish = Swish(0.1)

output =  swish(data)

plot_output(data, output, 'Swish')

LearningByDoing Series: Building Blocks of Neural Network - Activation Functions

Activation Functions:

Papers for Activation Functions

Sigmoid

What is the Sigmoid Function?

When is the Sigmoid Function Used?

What is the Math Formula of the Sigmoid Function?

Advantages and Disadvantages of the Sigmoid Function

Advantages:

Disadvantages:

Tanh

What is the Tanh Function?

When is the Tanh Function Used?

What is the Math Formula of the Tanh Function?

Advantages and Disadvantages of the Tanh Function

Advantages:

Disadvantages:

ReLU

What is the ReLU Function?

When is the ReLU Function Used?

What is the Math Formula of the ReLU Function?

Advantages and Disadvantages of the ReLU Function

Advantages:

Disadvantages:

LeakyReLU

What is the LeakyReLU Function?

When is the LeakyReLU Function Used?

What is the Math Formula of the LeakyReLU Function?

Advantages and Disadvantages of the LeakyReLU Function

Advantages:

Disadvantages:

Softmax

What is the softmax function?

When is the softmax function used?

What is the mathematical formula of the softmax function?

What are the advantages and disadvantages of softmax?

Advantages:

Disadvantages:

SoftPlus Activation Function

Formula

Usage

Advantages

Disadvantages

ELU

What is the ELU function?

When is the ELU function used?

What is the mathematical formula of the ELU function?

What are the advantages and disadvantages of ELU?

Advantages:

Disadvantages:

Not Zero-Centered for Positive Inputs: Similar to ReLU, the output of ELU for positive inputs is not zero-centered, which can potentially affect the convergence rate of gradient descent algorithms.

Mish

What is the Mish function?

When is the Mish function used?

What is the mathematical formula of the Mish function?

What are the advantages and disadvantages of Mish?

Advantages:

Disadvantages:

GELU

What is the GELU function?

When is the GELU function used?

What is the mathematical formula of the GELU function?

What are the advantages and disadvantages of GELU?

Advantages:

Disadvantages:

Swish

What is the Swish function?

When is the Swish function used?

What is the mathematical formula of the Swish function?

What are the advantages and disadvantages of Swish?

Advantages:

Disadvantages:

You may also enjoy:

LearningByDoing Series: Understanding effects of activation functions